How To Find Equation Of A Circle With Endpoints

Permit $$A\left( {{x_1},{y_1}} \right)$$ and $$B\left( {{x_2},{y_2}} \right)$$ be the cease points of the diameter of the circle as shown in the diagram.

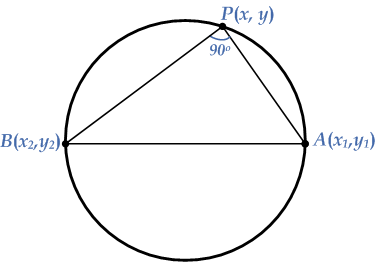
Let $$P\left( {ten,y} \right)$$ be any point of the circumvolve. Connecting the points $$A$$ and $$B$$ with the signal $$P$$ makes an bending $${ninety^ \circ }$$ betwixt them. Beginning we detect the slopes of the lines $$PA$$ and $$Lead$$ as:

Slope of the line $$PA = \frac{{y – {y_1}}}{{ten – {x_1}}}$$
Slope of the line $$PB = \frac{{y – {y_2}}}{{x – {x_2}}}$$

Since $$1000\angle APB = {ninety^ \circ }$$, the lines $$PA$$ and $$PB$$ are perpendicular to each other. Therefore, the product of their slopes is $$ – one$$. i.e.:

\[\begin{gathered} \frac{{y – {y_1}}}{{x – {x_1}}} \times \frac{{y – {y_2}}}{{x – {x_2}}} = – ane \\ \Rightarrow \frac{{\left( {y – {y_1}} \correct)\left( {y – {y_2}} \right)}}{{\left( {x – {x_1}} \right)\left( {ten – {x_2}} \correct)}} = – 1 \\ \Rightarrow \left( {y – {y_1}} \right)\left( {y – {y_2}} \correct) = – \left( {x – {x_1}} \right)\left( {x – {x_2}} \right) \\ \end{gathered} \]
\[ \Rightarrow \boxed{\left( {10 – {x_1}} \right)\left( {x – {x_2}} \correct) + \left( {y – {y_1}} \correct)\left( {y – {y_2}} \right) = 0}\]

This is the equation of the circumvolve through the extremities (ends) of its diameter. In order to find the centre and radius of this circle, we simplify the to a higher place equation of a circle as follows:

\[\begin{gathered} {x^2} – {x_1}x – {x_2}x + {x_1}{x_2} + {y^2} – {y_1}y – {y_2}y + {y_1}{y_2} = 0 \\ \Rightarrow {ten^2} + {y^2} – \left( {{x_1} + {x_2}} \right)x – \left( {{y_1} + {y_2}} \right)y + {x_1}{x_2} + {y_1}{y_2} = 0 \\ \end{gathered} \]

Comparing this equation with the full general equation of a circle, we have

\[one thousand = – \frac{{{x_1} + {x_2}}}{two},\,\,\,f = – \frac{{{y_1} + {y_2}}}{two},\,\,\,c = {x_1}{x_2} + {y_1}{y_2}\]

Therefore, the middle of the circumvolve is given past

\[\left( { – grand, – f} \correct) = \left( {\frac{{{x_1} + {x_2}}}{ii},\frac{{{y_1} + {y_2}}}{2}} \right)\]

The radius of the circle is given by

\[r = \sqrt {{g^2} + {f^2} – c} = \sqrt {{{\left( { – \frac{{{x_1} + {x_2}}}{2}} \right)}^2} + {{\left( { – \frac{{{y_1} + {y_2}}}{two}} \right)}^2} – \left( {{x_1}{x_2} + {y_1}{y_2}} \correct)} \]
\[\begin{gathered} \Rightarrow r = \sqrt {\frac{{{{\left( {{x_1} + {x_2}} \right)}^2} + {{\left( {{y_1} + {y_2}} \right)}^ii} – 4\left( {{x_1}{x_2} + {y_1}{y_2}} \right)}}{4}} \\ \Rightarrow r = \frac{{\sqrt {{x_1}^2 + {x_2}^2 + ii{x_1}{x_2} + {y_1}^2 + {y_2}^2 + two{y_1}{y_2} – 4{x_1}{x_2} – 4{y_1}{y_2}} }}{2} \\ \Rightarrow r = \frac{{\sqrt {{{\left( {{x_1} – {x_2}} \right)}^2} + {{\left( {{y_1} – {y_2}} \right)}^2}} }}{2} \\ \end{gathered} \]

Instance :
Find the equation of a circle through the ends $$\left( {5,vii} \right)$$ and $$\left( {1,3} \right)$$ of its bore. Also discover the middle and radius.

The equation of the circumvolve through the ends points of its diameter is

\[\left( {10 – {x_1}} \right)\left( {x – {x_2}} \correct) + \left( {y – {y_1}} \correct)\left( {y – {y_2}} \right) = 0\]

Here from the given points we have values $${x_1} = 5,\,\,{x_2} = 1,\,\,{y_1} = 7,\,\,{y_2} = 3$$
Now substitute these values of the given points in the to a higher place equation of a circle as

\[\brainstorm{gathered} \left( {x – 5} \right)\left( {x – 1} \correct) + \left( {y – 7} \right)\left( {y – 3} \right) = 0 \\ \Rightarrow {x^ii} – 6x + 5 + {y^2} – 10y + 21 = 0 \\ \Rightarrow {10^ii} + {y^ii} – 6x – 10y + 26 = 0 \\ \end{gathered} \]

The centre of the circle is $$\left( {\frac{{{x_1} + {x_2}}}{ii},\frac{{{y_1} + {y_2}}}{two}} \right) = \left( {\frac{{v + one}}{ii},\frac{{7 + three}}{2}} \right) = \left( {3,5} \right)$$

The radius of the circle is \[r = \frac{{\sqrt {{{\left( {{x_1} – {x_2}} \right)}^two} + {{\left( {{y_1} – {y_2}} \correct)}^2}} }}{2} = \frac{{\sqrt {{{\left( {v – 1} \right)}^ii} + {{\left( {7 – 3} \right)}^ii}} }}{2} = \frac{{4\sqrt ii }}{2} = 2\sqrt 2 \]